第三章 树和二叉树
作者:whisper
链接:http://proprogrammar.com:443/article/56
声明:请尊重原作者的劳动,如需转载请注明出处
说明:本章主要讲树和二叉树(定义,性质,存储结构,遍历),线索二叉树,树和森林的表示方法,树和森林的遍历,哈夫曼树与哈夫曼编码
树的类型定义
数据对象 D:
D 是具有相同特性的数据元素的集合。
数据关系 R:
若 D 为空集,则称为空树;
否则:
(1) 在 D 中存在唯一的称为根的数据元素 root,
基本操作:查找类、插入类、删除类
查找类:
Root(T); // 求树的根结点
Parent(T, cur_e); // 求当前结点的双亲结点
RightSibling(T, cur_e); // 求当前结点的右兄弟
TreeDepth(T); // 求树的深度
插入类:
CreateTree(&T, definition); // 按定义构造树
InsertChild(&T, &p, i, c); // 将以 c 为根的树插入为结点 p 的第 i 棵子树
删除类:
DestroyTree(&T); // 销毁树的结构
例如:

有向树:
(1) 有确定的根;
(2) 树根和子树根之间为有向关系。
有序树:
子树之间存在确定的次序关系。
注:二叉树不等价于度不大于2的有序树,因为当这个有序树只有一个子树时,不分区分是左子树还是右子树
无序树:
子树之间不存在确定的次序关系。
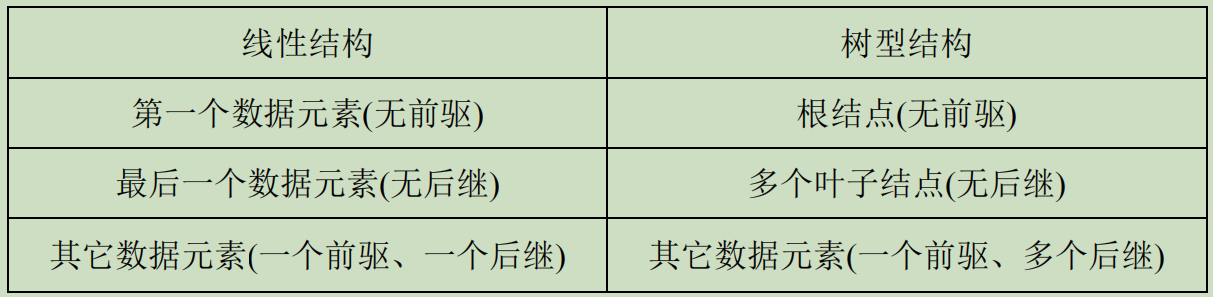
对比树型结构和线性结构的结构特点:
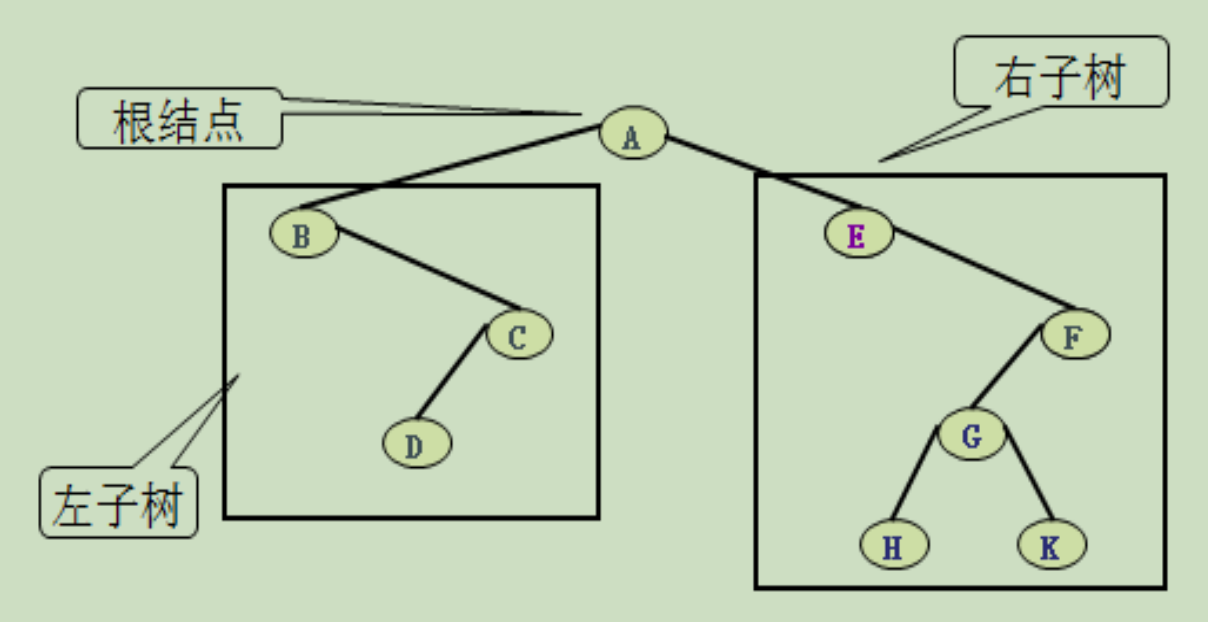
二叉树的类型定义
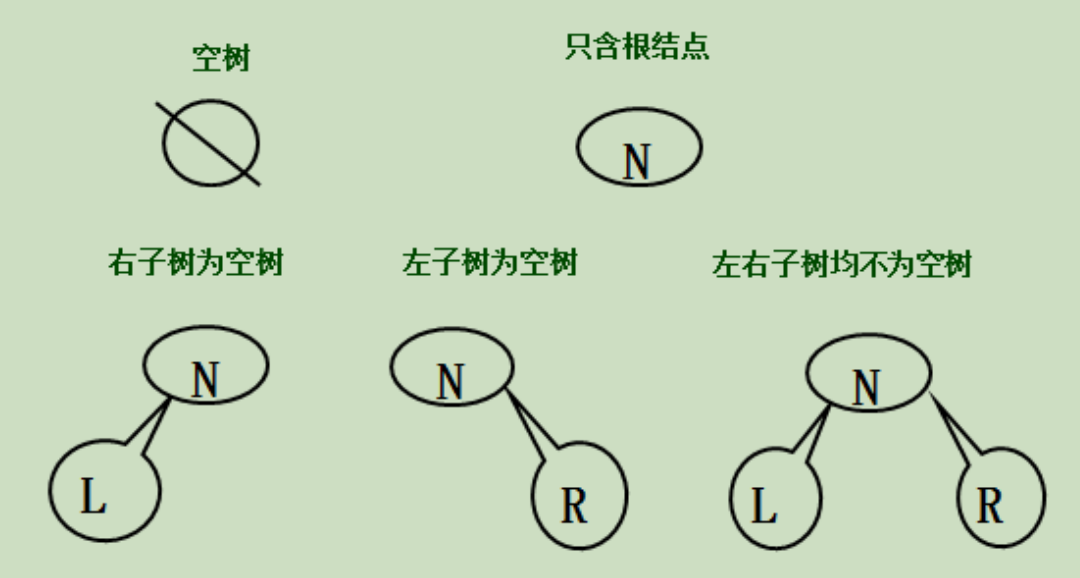
(二)二叉树的主要基本操作:查找类、插入类、删除类
查找类:
插入类:
删除类:
(三)二叉树的重要特性
性质 1 : 在二叉树的第 i 层上至多有 2^(i-1) 个结点。 (i≥1)
e.g. 有 n 个结点且高度为 n 的二叉树有多少种? 2^(n-1)种
推广: 满二叉树第 k 层的结点个数比其第 1~k-1 层所有的结点总数多 1 个。
证明:设 二叉树上结点总数 n = n0 + n1 + n2
又 二叉树上分支总数 b = n1+ 2n2
而 b = n-1 = n0 + n1 + n2 - 1
由此, n0 = n2+ 1
证明:设 N 为总结点数,N0 为叶子结点数,
则: N=N0+N1+N2+……+Nm
又有:N-1=分支总数,
则:N-1=N1*1+N2*2+……Nm*m
则有:N0=1+N2+2N3+……+(m-1)Nm
两类特殊的二叉树:
满二叉树:深度为 k 且含有 2ᵏ -1 个结点的二叉树。
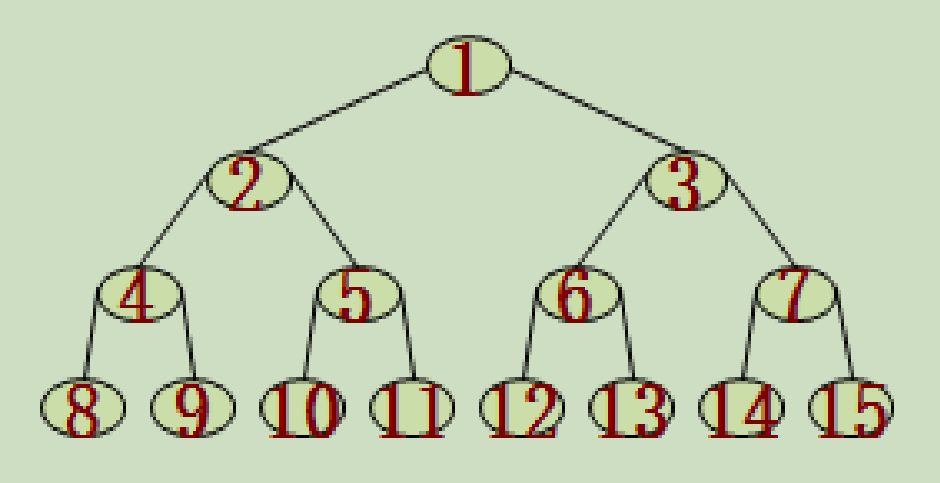
完全二叉树:树中所含的 n 个结点和满二叉树中编号为 1 至 n 的结点一一对应。
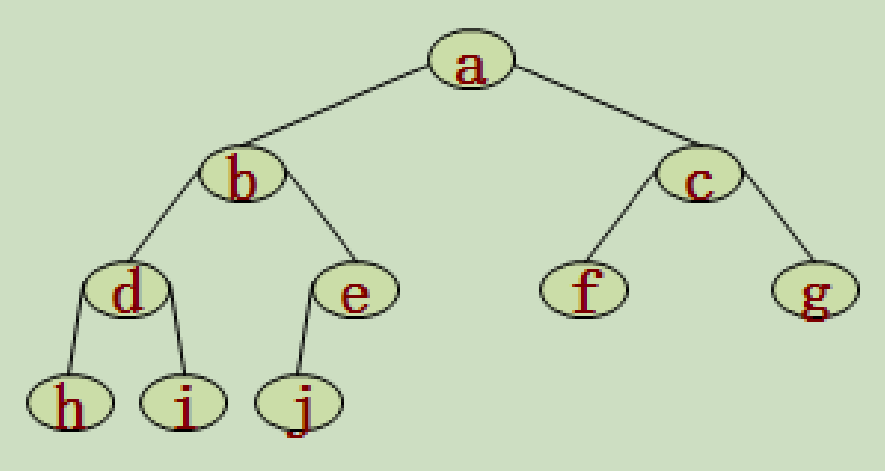
推广: 对于一棵有 n 个结点的完全二叉树:
(2)若 n 为偶数,则树中除了 度为 0 和度为 2 的结点,还有 1 个度为 1 的结点。
性质 4 :具有 n 个结点的完全二叉树的深度为 ⌊log2n⌋ +1。
证明:设 完全二叉树的深度为 k
则根据第二条性质得 2^(k-1)≤ n < 2^k即 k-1 ≤ log2 n < k
因为 k 只能是整数,因此,k =⌊log2n⌋ + 1
注:又n <= 2^k - 1 即 log2 (n+1) <= k,即k = ⌈log2 (n+1)⌉
(1) 若 i=1,则该结点是二叉树的根,无双亲, 否则,编号为 ⌊i/2⌋ 的结点为其双亲结点;
(3) 若 2i+1>n,则该结点无右孩子结点,否则,编号为 2i+1 的结点为其右孩子结点。
二叉树的存储结构
(一)二叉树的顺序存储表示
#define MAX_TREE_SIZE 100 // 二叉树的最大结点数
typedef TElemType SqBiTree[MAX_TREE_SIZE]; // 0 号单元存储根结点
例如:
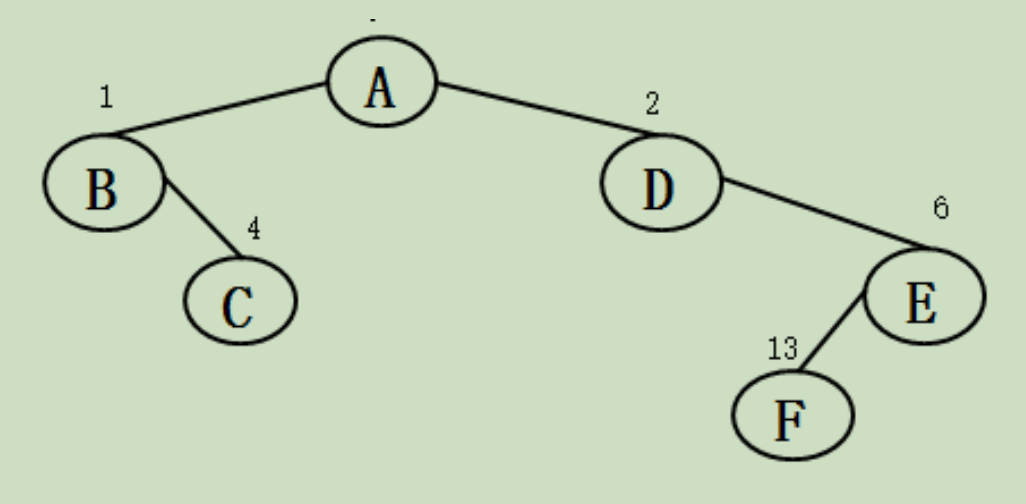

(二)二叉树的链式存储表示
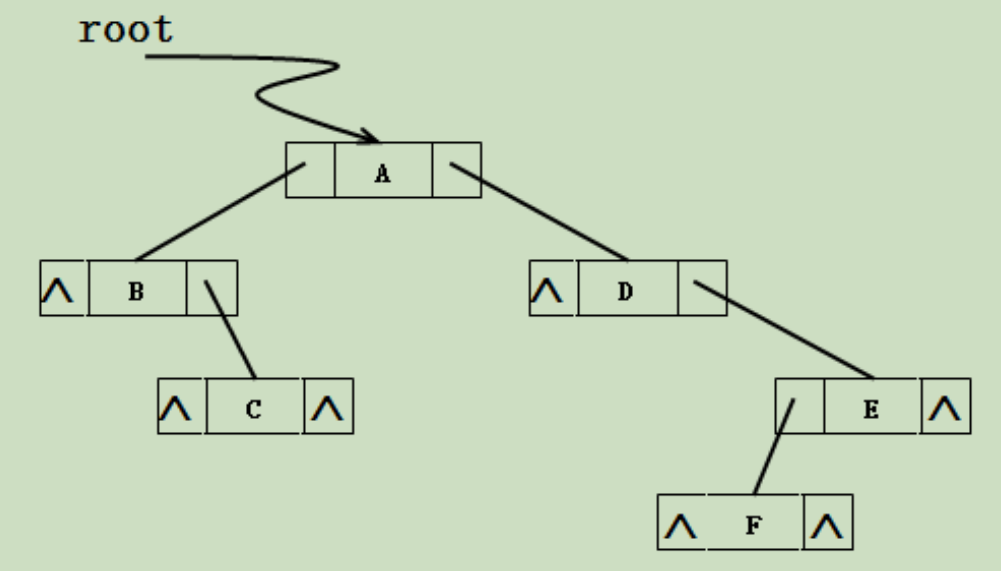
结点结构:

TElemType data;
} BiTNode, *BiTree;
2.三叉链表
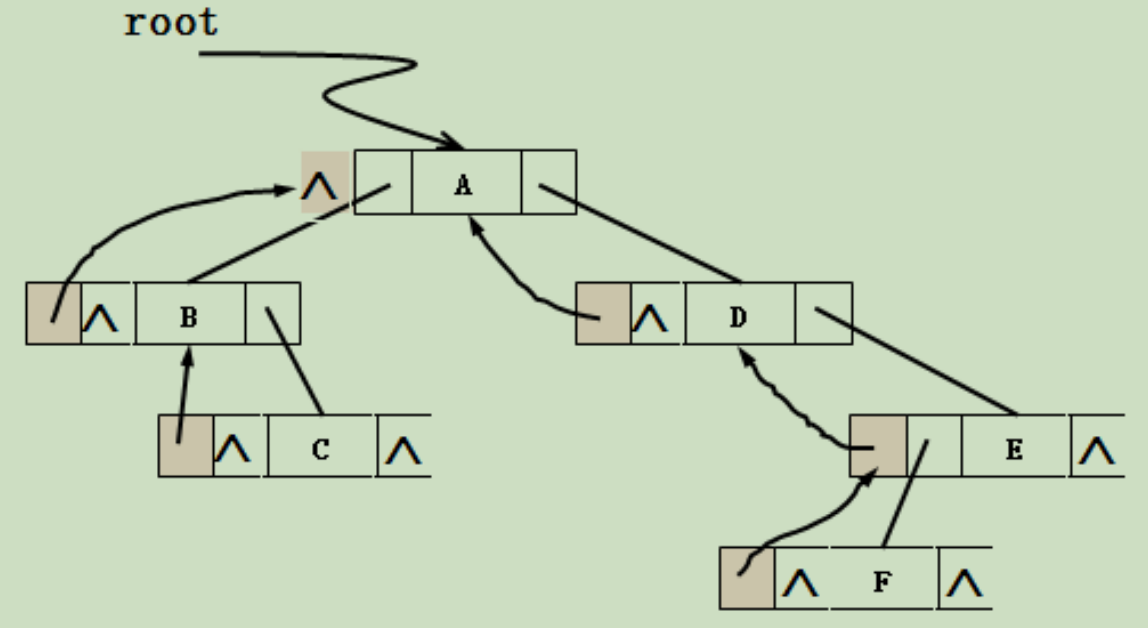
结点结构:

C 语言的类型描述如下:
TElemType data;
struct TriTNode *parent; //双亲指针
若一个二叉树含有 n 个结点,则它的二叉链表中必含有 2n 个指针域, 其中必有 n+1 个空的链域。
证明:分支数目 B=n-1,即非空的链域有 n-1 个,故空链域有 2n-(n-1)=n+1 个。不同的存储结构实现二叉树的操作也不同。如要找某个结点的父结点,在三叉链表中很容易实现;在二叉链表中则需从根指针出发一一查找。可见,在具体应用中,需要根据二叉树的形态和需要进行的操作来决定二叉树的存储结构。
注意:
二叉树的遍历
顺着某一条搜索路径巡访二叉树中的结点,使得每个结点均被访问一次,而且仅被访问一次。
“访问”的含义可以很广,如:输出结点的信息等。
对“二叉树”而言,可以有三条搜索路径:
2.先左(子树)后右(子树)的遍历;
(二)先左后右的遍历算法
中(根)序的遍历算法
后(根)序的遍历算法
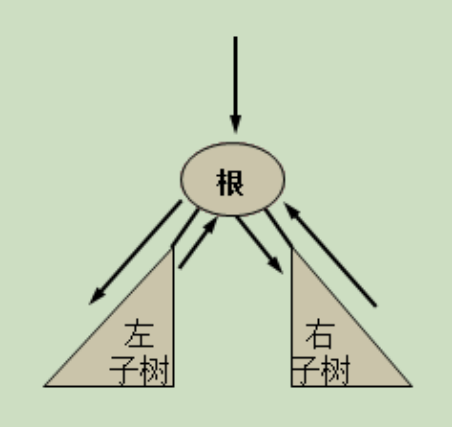
若二叉树为空树,则空操作;否则,
(2)先序遍历左子树;
中(根)序的遍历算法:
(1)中序遍历左子树;
(3)中序遍历右子树。
若二叉树为空树,则空操作;否则,
(2)后序遍历右子树;
(三)算法的递归描述
void Preorder (BiTree T,void( *visit)(TElemType& e)) // 先序遍历二叉树
{
if (T) {
visit(T->data); // 访问结点
Preorder(T->lchild, visit); // 遍历左子树
Preorder(T->rchild, visit); // 遍历右子树
}
}(四)中序、先序、后序遍历算法的非递归描述
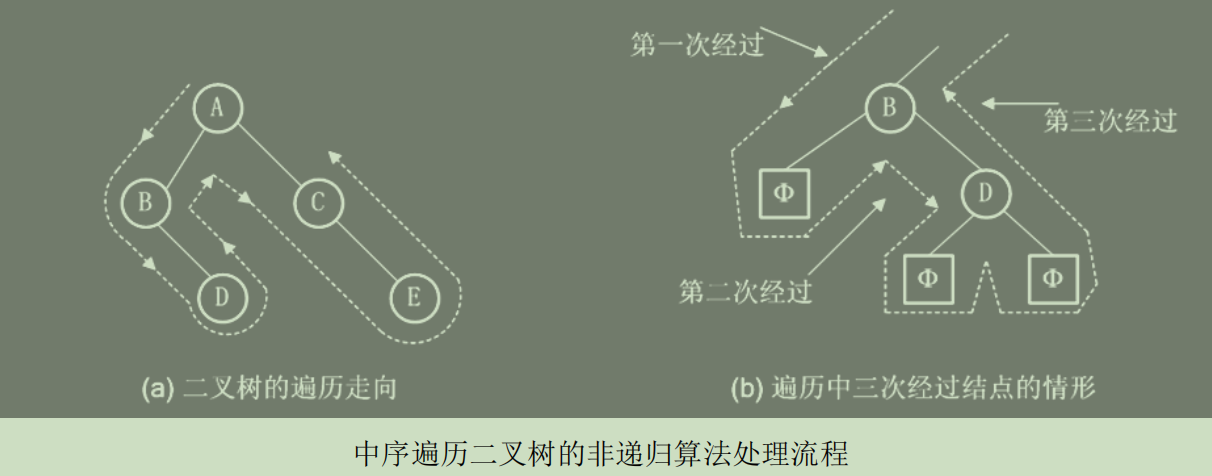
中序遍历非递归算法:
然后出栈一个结点,显然该结点没有左孩子结点或者左孩子结点已访问过,则访问它。
中序遍历二叉树的非递归算法(调用栈操作的函数)
void InOrder(BiTree root){
InitStack (&S);
p=root;
while(p! =NULL || !StackEmpty(S))
{
if (p! =NULL){ /* 根指针进栈, 遍历左子树 */
Push(&S, p);
p=p->LChild;
}
else
{ /*根指针退栈, 访问根结点, 遍历右子树*/
Pop(&S, p); Visit(p->data);
p=p->RChild;
}
}
}中序遍历二叉树的非递归算法(直接实现栈操作)
void NRInOrder(BiTree bt){
BiTree Stack[MAX_TREE_SIZE],p;
int top=0; p=bt;
if (bt==NULL) return;
while(!(p==NULL&&top==0)) {
while(p!=NULL) {
if(top< MAX_TREE_SIZE-1){ //将当前指针 p 压栈
Stack[top++]=p;
else {
printf(“栈溢出”);
return;
}
p=p->lchild; //指针指向 p 的左孩子结点
}
if (top<=0) return; //栈空时结束
else {
p=Stack[- -top]; //从栈中弹出栈顶元素
Visit(p->data); //访问结点的数据域
p=p->rchild; //指针指向 p 的右孩子结点
}
}
}注:觉得这里写得不好,写得逻辑和调用栈操作不统一,应该写得一样好理解
先序非递归算法:
由先序遍历过程可知,先访问根结点,再访问左子树,最后访问右子树。
void PreOrder1(BiTree b){
BiTree St[MAX_TREE_SIZE],p; int top=-1;
if (b!=NULL) {
St[++top]=b; //根结点进栈
while (top>-1){ //栈不空时循环
p=St[top--]; //出栈并访问该结点
Visit(p->data);
if (p->rchild!=NULL) //右孩子结点进栈
St[++top]= p->rchild;
if (p->lchild!=NULL) //左孩子结点进栈
St[++top]= p->lchild;
}
}
}后序遍历非递归算法:
当一个结点的左、右孩子结点均被访问后再访问该结点,如此这样,直到栈空为止。
从上述过程可知,栈中保存的是当前结点*b 的所有祖先结点(均未访问过)。
void PostOrder1(BiTree b){
BiTree St[MAX_TREE_SIZE],p;
int flag,top=-1;
if (b!=NULL) {
do{
while(b!=NULL) { //扫描*b 的左结点并进栈
St[++top]=b;
b=b->lchild;
}
p=NULL; //p 指向栈顶结点的前一个已访问的结点
flag=1; //设置 b 的已访问标记为已访问过
while(top!=-1&&flag){
b=St[top]; //取出当前的栈顶元素
if (b->rchild == null || b->rchild==p){
//右孩子不存在或右孩子已被访问,则访问*b
Visit(b->data); //访问*b 结点
top--;
p=b; //p 指向被访问的结点
}
else{
b=b->rchild; //b 指向右孩子结点
flag=0; //设置未被访问的标记
}
}
}while(top!=-1);
}
}
由二叉树的先序和中序序列建树
二叉树的先序序列 根-左子树-右子树
注:知道先序和中序,后序和中序都可以惟一确定一棵二叉树,但知道先序和后序并不能惟一确定一棵二叉树
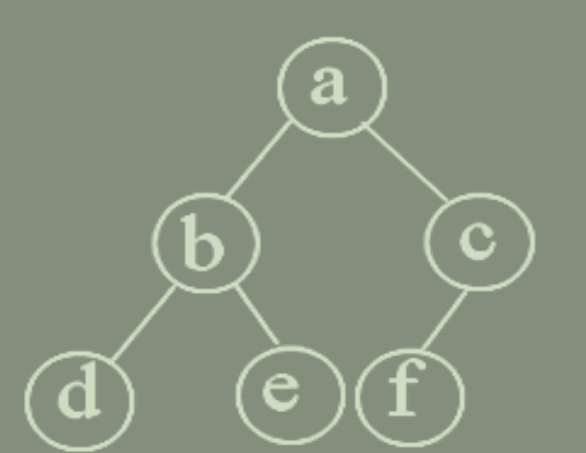
例如:
先序序列 abcdefg
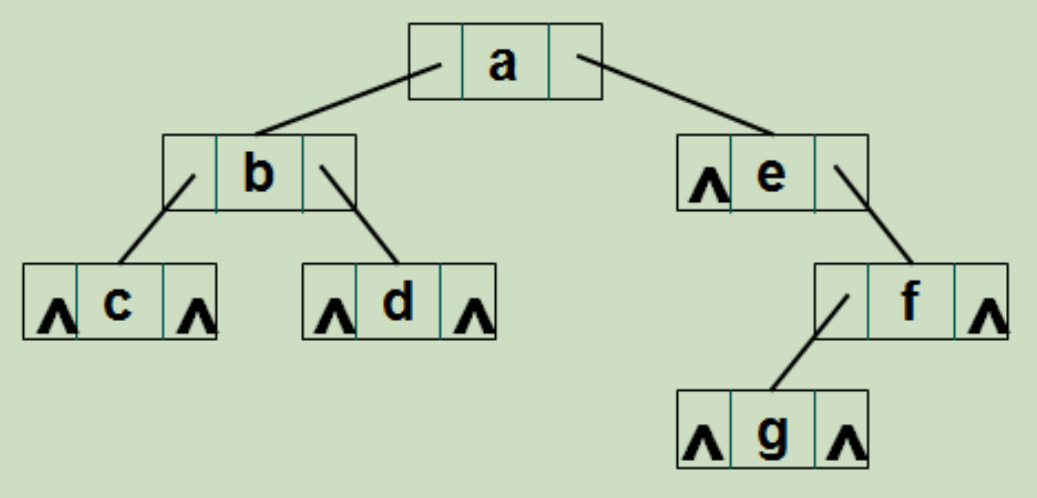
1、查询二叉树中某个结点
(2) 否则在左子树中进行查找,若找到,则返回 TRUE;
Status PreorderSearch (BiTree T, ElemType x, BiTree &p) {
// 若二叉树中存在和 x 相同的元素,
//则 p 指向该结点并返回 OK,否则返回 FALSE
if (T) {
if (T->data==x) { p = T; return OK;}
else {
if (PreorderSearch(T->lchild, x, p) return OK;
else return(PreorderSearch(T->rchild, x, p)) ;
}//else
}//if
else return FALSE;
}
算法基本思想: 先序(或中序或后序)遍历二叉树,在遍历过程中查找叶子结点,并计数。由此,需在遍历算法中增添一个“计数”的参数,并将算法中“访问结点” 的操作改为:若是叶子,则计数器增 1。
void CountLeaf (BiTree T, int &count){
if ( T ) {
if ((!T->lchild)&& (!T->rchild))
count++; // 对叶子结点计数
CountLeaf( T->lchild, count);
CountLeaf( T->rchild, count);
} // if
} // CountLeaf
/* LeafCount 是保存叶子结点数目的全局变量, 调用之前初始化值为 0 */
void leaf(BiTree T){
if(T) {
leaf(T->LChild);
leaf(T->RChild);
if ((!T->lchild)&& (!T->rchild)) LeafCount++;
}
}
int CountLeaf (BiTree T){
//返回指针 T 所指二叉树中所有叶子结点个数
if (!T ) return 0;
if (!T->lchild && !T->rchild) return 1;
else{
m = CountLeaf( T->lchild);
n = CountLeaf( T->rchild);
return (m+n);
}
}拓展:返回指针 T 所指二叉树中所有结点个数
int Count (BiTree T){
//返回指针 T 所指二叉树中所有结点个数
if (!T ) return 0;
if (!T->lchild && !T->rchild) return 1;
else{
m = Count ( T->lchild);
n = Count ( T->rchild);
return (m+n+1);
}
}
算法基本思想: 首先分析二叉树的深度和它的左、右子树深度之间的关系。
int Depth (BiTree T ){ // 返回二叉树的深度
if ( !T ) depthval = 0;
else {
depthLeft = Depth( T->lchild );
depthRight= Depth( T->rchild );
depthval =1+(depthLeft>depthRight?depthLeft:depthRight);
}
return depthval;
}4、复制二叉树(后序遍历)
其基本操作为:生成一个结点。
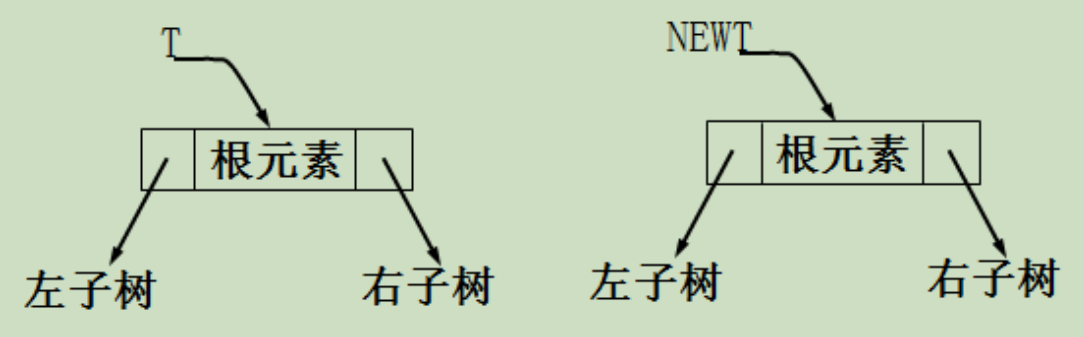
生成一个二叉树的结点(其数据域为 item,左指针域为 lptr,右指针域为 rptr)
BiTree GetTreeNode(TElemType item, BiTNode *lptr , BiTNode *rptr ){
if (!(T = new BiTNode))
exit(1);
T-> data = item;
T-> lchild = lptr;
T-> rchild = rptr;
return T;
}
BiTree CopyTree(BiTNode *T) {
if (!T ) return NULL;
if (T->lchild ) newlptr = CopyTree(T->lchild); //复制左子树
else newlptr = NULL;
if (T->rchild ) newrptr = CopyTree(T->rchild); //复制右子树
else newrptr = NULL;
newT = GetTreeNode(T->data, newlptr, newrptr);
return newT;
} // CopyTree例如:下列二叉树的复制过程如下:
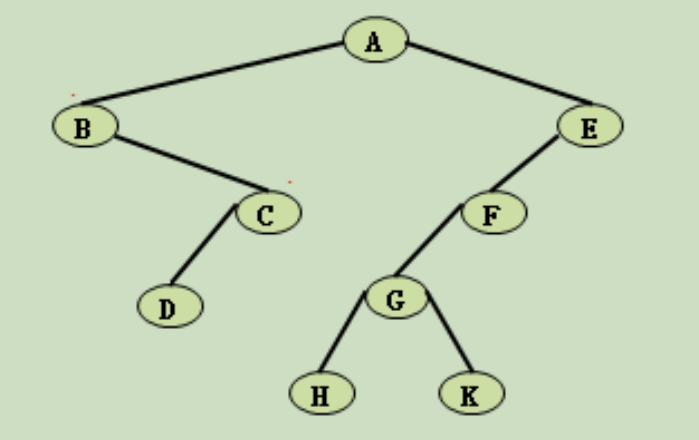
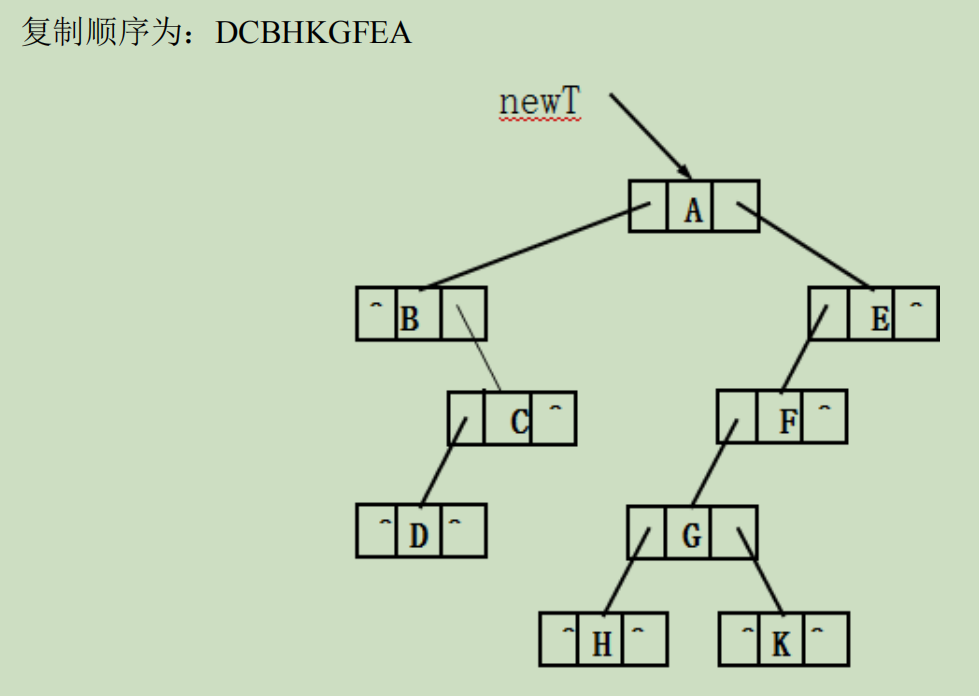
5、建立二叉树的存储结构
不同的定义方法相应有不同的存储结构的建立算法。
以字符串的形式 “根 左子树 右子树”定义一棵二叉树。
例如:
空树 以空白字符 表示
表示
只含一个根结点的二叉树 以字符串A
 表示
表示

Status CreateBiTree(BiTree &T) {
scanf(&ch);
if (ch=='') T = NULL;
else {
if (!(T = new BiTNode))
exit(OVERFLOW);
T->data = ch; // 生成根结点
CreateBiTree(T->lchild); // 构造左子树
CreateBiTree(T->rchild); // 构造右子树
}
return OK;
} // CreateBiTree算法执行过程举例如下:
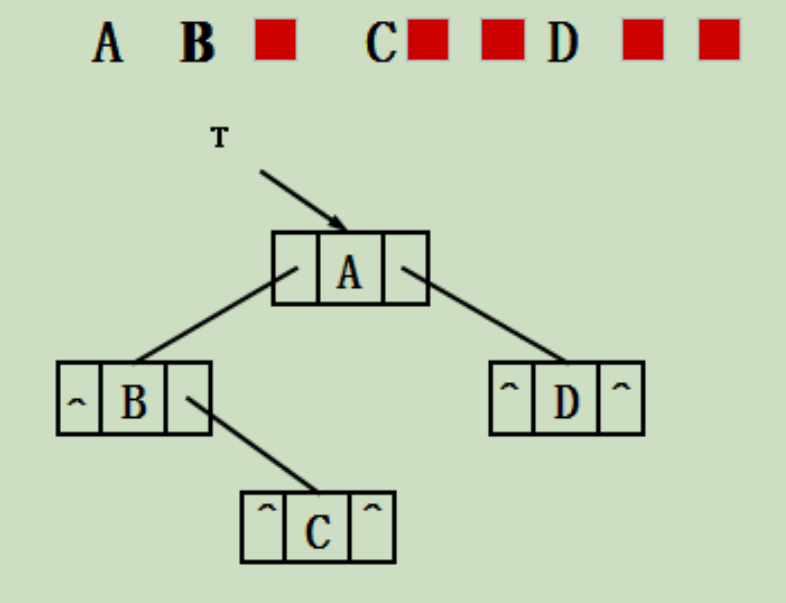
例如:通过先序和中序序列构造一棵二叉树
先序序列 abcdefg
中序序列 cbdaegf
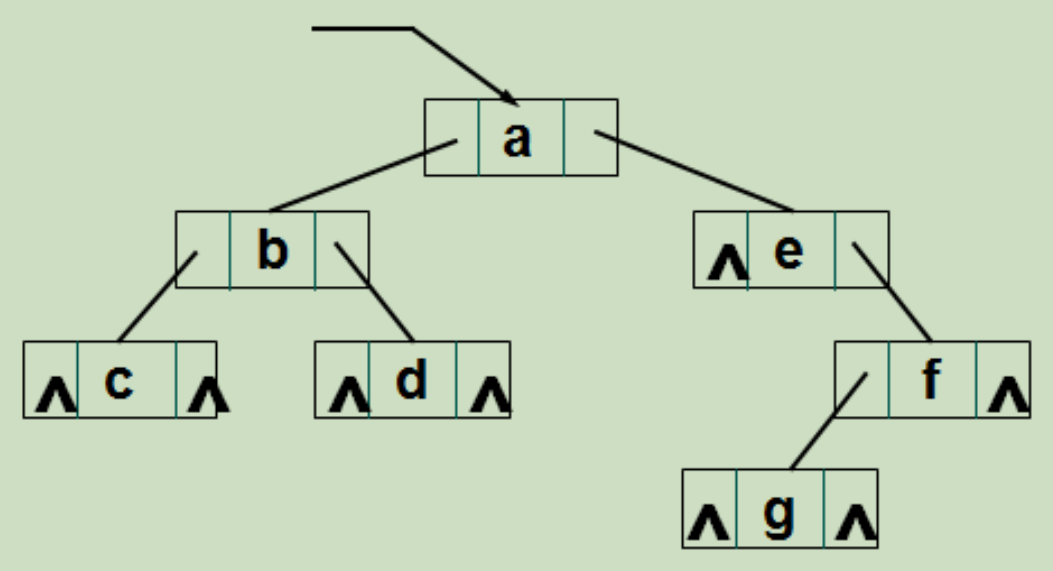
void CrtBT(BiTree& T, char pre[], char ins[],int ps, int is, int n ) {
// 已知 pre[ps..ps+n-1]为二叉树的先序序列,
// ins[is..is+n-1]为二叉树的中序序列,本算
// 法由此两个序列构造二叉链表
if (n==0) T=NULL;
else {
k=Search(ins, pre[ps]); // 在中序序列中查询先序中元素的索引
if (k== -1) T=NULL;
else {
if (!(T= new BiTNode)) exit(OVERFLOW);
T->data = pre[ps];
if (k==is) T->Lchild = NULL;
else CrtBT(T->Lchild, pre[], ins[], ps+1, is, k-is );
if (k=is+n-1) T->Rchild = NULL;
else CrtBT(T->Rchild, pre[], ins[], ps+1+(k-is), k+1, n-(k-is)-1 );
}
} //
} // CrtBT
注:对先序序列,元素顺序为双亲结点,左子树,右子树
对中序序列,元素顺序为左子树,双亲结点,右子树
6、按给定的表达式建相应二叉树
由先缀表示式建树
例如:已知表达式的先缀表示式-×+ a b c / d e
由原表达式建树
例如:已知表达式 (a+b)×c – d/e
对应先缀表达式-×+ a b c / d e 的二叉树
特点:操作数为叶子结点,运算符为分支结点
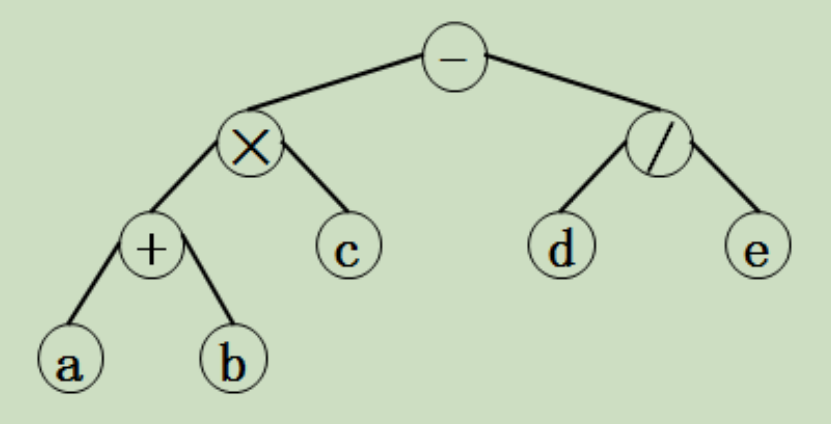
分析表达式和二叉树的关系:
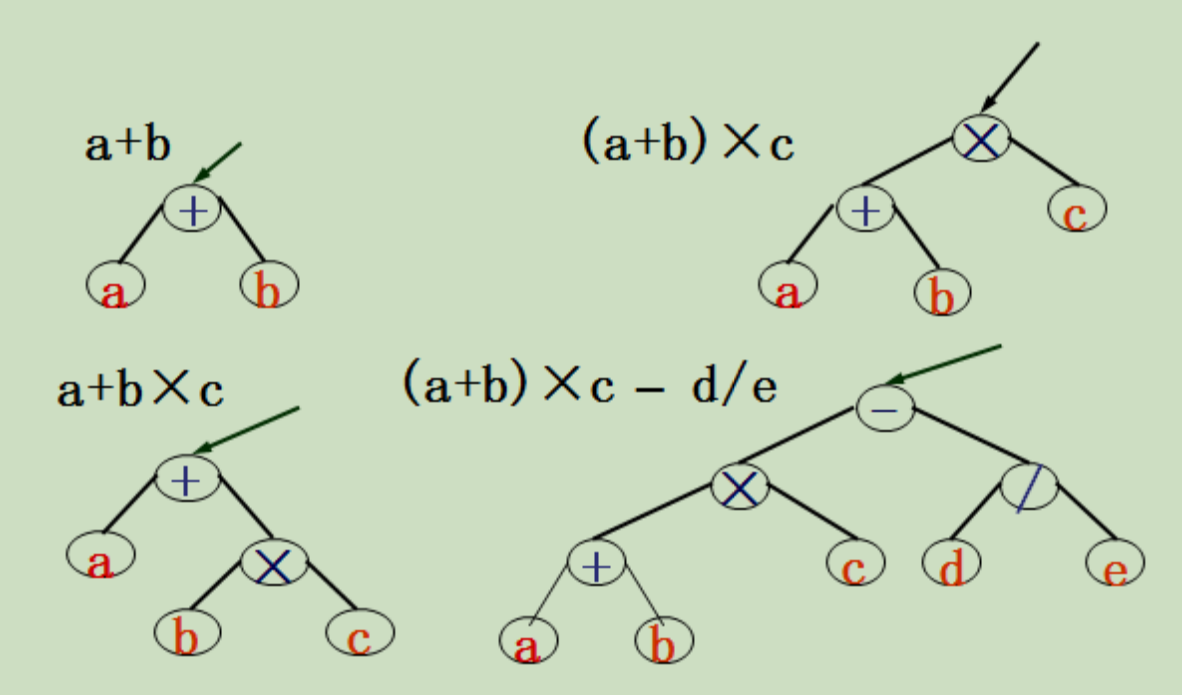
例:假设一个仅包含二元运算符的算术表达式以链表形式存储在二叉树 BT 中,写出计算该算术表达式值的算法。
typedef struct node{
ElemType data;
float val;
char optr; //只取‘+’, ‘-’, ‘*’,‘/’
struct node *lchild,*rchild ;
}BiNode,*BiTree;
float PostEval(BiTree bt) // 以后序遍历算法求以二叉树表示的算术表达式的值
{
float lv,rv,value;
if(bt!=null)
{
if(bt.data == 1){// 该结点为操作符结点
lv=PostEval(bt->lchild); // 求左子树表示的子表达式的值
rv=PostEval(bt->rchild); // 求右子树表示的子表达式的值
switch(bt->optr)
{
case ‘+’: value=lv+rv; break;
case ‘-’: value=lv-rv;break;
case ‘*’: value=lv*rv;break;
case ‘/’: value=lv/rv;
}
else{ // 该结点为操作数结点
value = bt.val;
}
}
return(value);
}
由层次遍历的定义可知,在进行层次遍历时,对一层结点访问完后,再按照它们的访问次序对各个结点的左孩子和右孩子顺序访问,这样一层一层进行,先遇到的结点先访问,这与队列的操作原则比较吻合。
①访问该元素所指结点;
此过程不断进行,当队列为空时,二叉树的层次遍历结束。
一维数组 Queue[MAX_TREE_SIZE]用以实现队列,变量 front 和 rear 分别表示当前队首元素和队尾元素在数组中的位置。
void LevelOrder(BiTree b){
BiTree Queue[MAX_TREE_SIZE];
int front,rear;
if (b==NULL) return;
front=-1; rear=0;
Queue[rear]=b;
while(front!=rear) {
Visit(Queue[++front]->data); //访问队首结点数据域
if (Queue[front]->lchild!=NULL)
//将队首结点的左孩子结点入队列
Queue[++rear]= Queue[front]->lchild;
if (Queue[front]->rchild!=NULL)
//将队首结点的右孩子结点入队列
Queue[++rear]= Queue[front]->rchild;
}
}遍历二叉树是二叉树各种操作的基础。二叉树的操作包括插入和删除,以及二叉树的复制和左、右子树之间的交换,其核心思想是选择合适的遍历方式进行操作,大部分操作需要借助循环或递归完成。熟悉二叉树的性质、存储结构特点和遍历算法的基础上,可比较容易解决此类问题。
小结:满足下列条件的二叉树:
(1)若先序序列与后序序列相同,则或为空树,或为只有根结点的二叉树。
(2)若中序序列与后序序列相同,则或为空树,或为任一结点至多只有左子树的二叉树。
(3)若先序序列与中序序列相同,则或为空树,或为任一结点至多只有右子树的二叉树。
(4)若中序序列与层次遍历序列相同,则或为空树,或为任一结点至多只有右子树的二叉树。
线索二叉树
(一)何谓线索二叉树?
遍历二叉树的结果是,求得结点的一个线性序列。
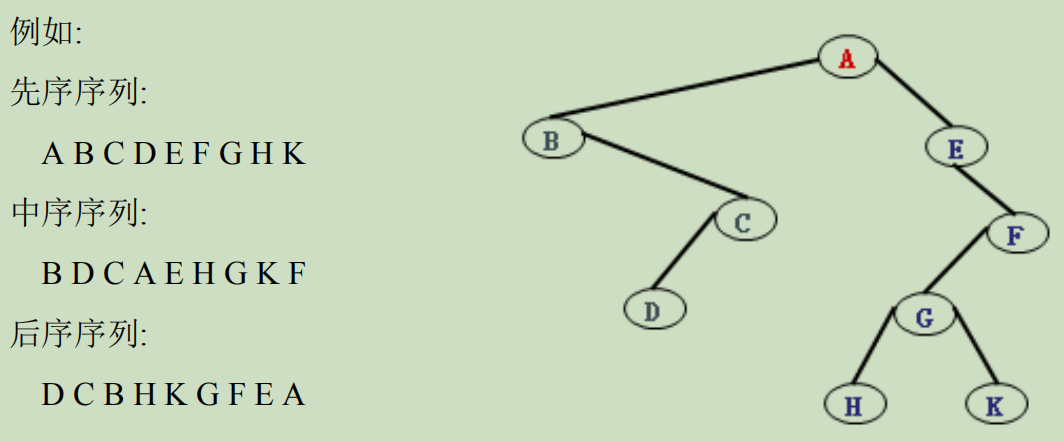
指向该线性序列中的“前驱”和“后继” 的指针,称作“线索”
包含 “线索” 的存储结构,称作 “线索链表”
与其相应的二叉树,称作 “线索二叉树”
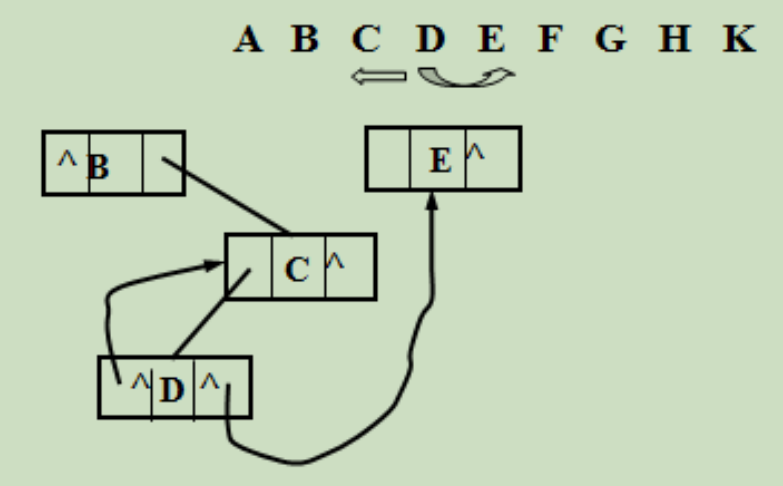
对线索链表中结点的约定:
在二叉链表的结点中增加两个标志域,并作如下规定:
若该结点的右子树不空,则 rchild 域的指针指向其右子树,且右标志域的值为“指针 Link”;否则,rchild 域的指针指向其“后继”,且右标志的值为“线索Thread”。
如此定义的二叉树的存储结构称作“线索链表”
线索链表的类型描述:
typedef enum { Link, Thread } PointerThr;
// Link==0:指针,Thread==1:线索
typedef struct BiThrNod {
TElemType data;
struct BiThrNode *lchild, *rchild; // 左右指针
PointerThr LTag, RTag; // 左右标志
} BiThrNode, *BiThrTree;(二)线索链表的遍历算法:
for ( p = firstNode(T); p; p = Succ(p) )
Visit (p);例如:对中序线索化链表的遍历算法
中序遍历的第一个结点 ?
左子树上处于“最左下”(没有左子树)的结点
在中序线索化链表中结点的后继?
在中序线索二叉树中找后继结点
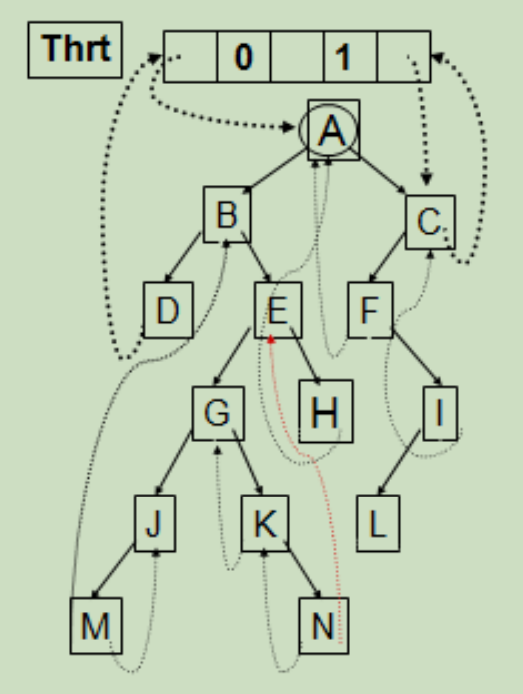
中序遍历二叉线索树的过程分析(I)
2.从根结点 A 开始,找到其左孩子,左孩子的左孩子,…,直到某个结点(即 D)的LTag==1
4.如果某个结点的 RTag==0 则说明该结点有右子树,此时应该访问其右子树,转到第二步,只是此时是从右子树开始
Status InOrderTraverse_Thr(BiThrTree T, Status(*Visit)(TElemType)) {
//T 指向头结点,头结点的 lchild 左链指向根结点
//中序遍历二叉线索树的非递归算法
p=T–>lchild; //p 指向根结点
while (p!=T) { //空树或遍历结束时 p==T
while (p –>LTag ==Link) p=p –>lchild;
if (!Visit(p –>data)) return ERROR; //访问左子树为空的结点
while (p –>RTag ==Thread && p –>rchild!=T) {
p=p –>rchild; Visit(p –>data); // 访问后继结点
}
p= p–>rchild; //如果 p->RTag==Link,则从其右子树开始
}
return OK;
}//InOrderTraverse_Thr在中序线索二叉树中找前驱结点
由中序遍历的规律可知,作为根 p 的前驱结点,它是中序遍历 p 的左子树时访问的最后一个结点,即左子树的“最右下端”结点。
若结点 p 是二叉树的根,则 p 的前驱为空;
若 p 是双亲的右孩子且双亲有左孩子,则 p 的前驱是其双亲的左子树中按先序遍历时最后访问的那个结点。
在先序线索二叉树中找后继结点
根据先序线索树的遍历过程可知,
2.若结点 p 没有左子树,但有右子树,则 p 的右孩子结点即为 p 的后继;
在后序线索二叉树中找前驱结点
根据后序线索树的遍历过程可知,
2.若结点 p 存在左子树,但无右子树,则其前驱是左子树的根;
在后序线索二叉树中找后继结点
可分为 3 种情况:
2.若结点 p 是其双亲的右孩子或是其双亲的左孩子且其双亲没有右子树,则其后继即为双亲结点;
(三)如何建立线索链表?
线索化的实质是将二叉链表中的空指针改为指向前驱或后继的线索。
因此,线索化的过程即为在遍历过程中修改空指针的过程。
Status InOrderThreading(BiThrTree &Thrt, BiThrTree T) {
//中序遍历二叉树 T,并将其中序线索化,Thrt 指向头结点
if (!Thrt = (BiThrTree)malloc(sizeof(BiThrNode)))
exit (OVERFLOW);
Thrt->LTag=Link; Thrt->RTag=Thread; //建立头结点
Thrt->rchild=Thrt; //右指针回指
if (!T) Thrt->lchild=Thrt; //若二叉树空,左指针回指
else { Thrt->lchild=T; pre=Thrt;
InThreading(T); //中序遍历进行中序线索化
pre->rchild=Thrt; //最后一个结点线索化
pre->RTag=Thread;
Thrt->rchild=pre;
}
return OK;
}
Status InThreading(BiThrTree &p) {
//中序遍历进行中序线索化
if (p) {
InThreading(p->lchild); //左子树线索化
if (!p->lchild) {
p->LTag=Thread;p->lchild=pre;
} //前驱线索
if (!pre->rchild) {
pre->RTag=Thread; pre->rchild=p;
}//后继线索
pre=p; //保持 pre 指向 p 的前驱
InThreading(p->rchild); //右子树线索化
}
return OK;
}//InOrderThreading线索二叉树:在二叉链表表示的二叉树中,引入线索的目的主要是便于查找结点的前驱和后继。因为若知道各结点的后继,二叉树的遍历就变得非常简单。
由于序列可由不同的遍历方法得到,因此,线索树有先序线索二叉树、中序线索二叉树和后序线索二叉树三种。
在先序、中序和后序线索二叉树中所有实现均相同,即线索化之前的二叉树相同,所有结点的标志位取值也完全相同,只是当标志位取 1 时,不同的线索二叉树将用不同的虚线表示,即不同的线索树中线索指向的前驱结点和后继结点不同。
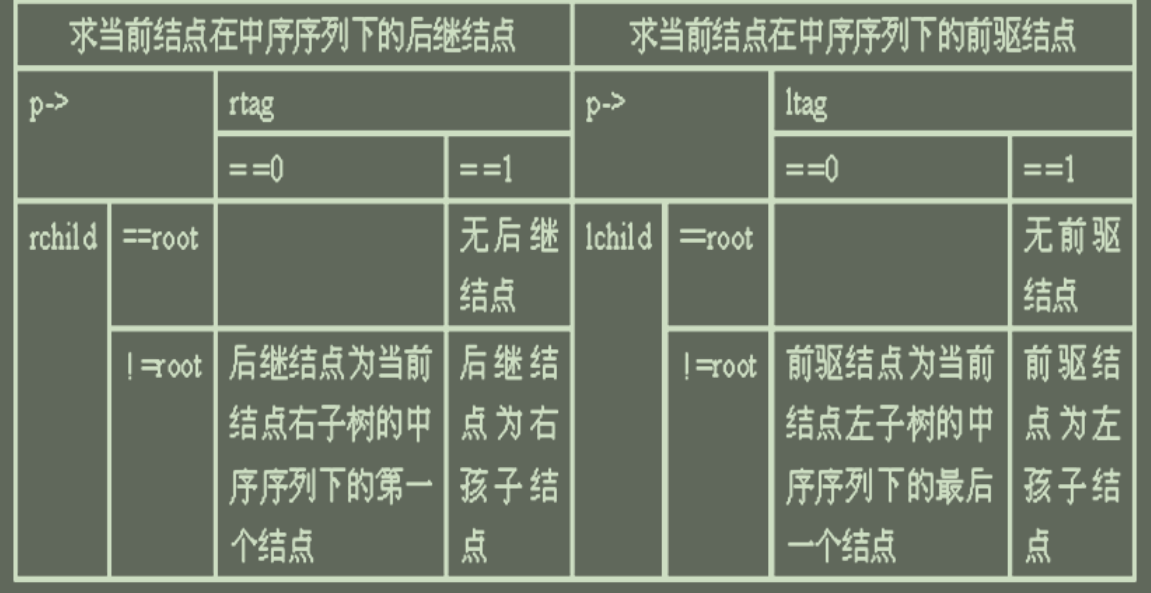
注:右子树的中序序列下的第一个结点:右子树最左结点;左子树的中序序列下的最后一个结点:左子树最右结点
树和森林的表示方法
(一)树的三种存储结构
1.双亲表示法(顺序表示法):
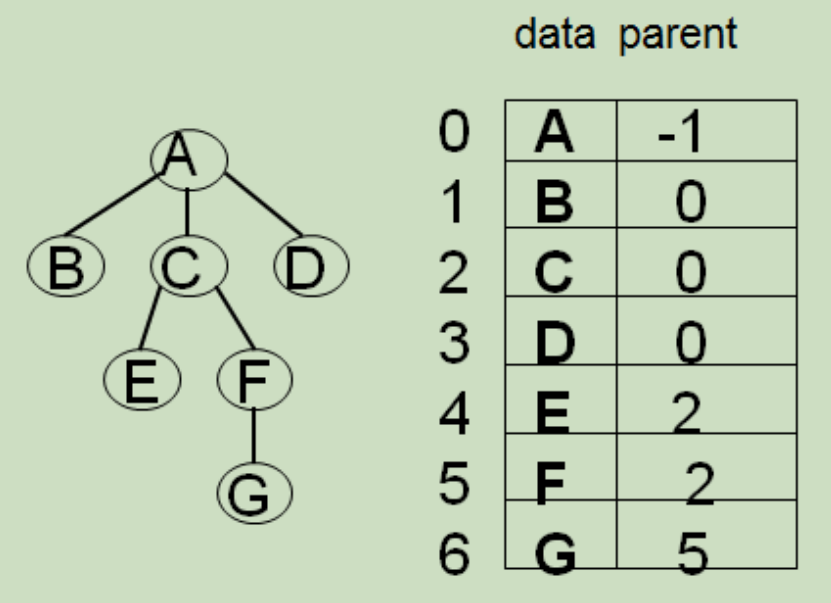
结点结构:

C 语言的类型描述:
#define MAX_TREE_SIZE 100
typedef struct PTNode {
Elem data;
int parent; // 双亲位置域
} PTNode;
typedef struct {
PTNode nodes [MAX_TREE_SIZE];
int r, n; // 根结点的位置和结点个数
} PTree;2.孩子链表表示法:
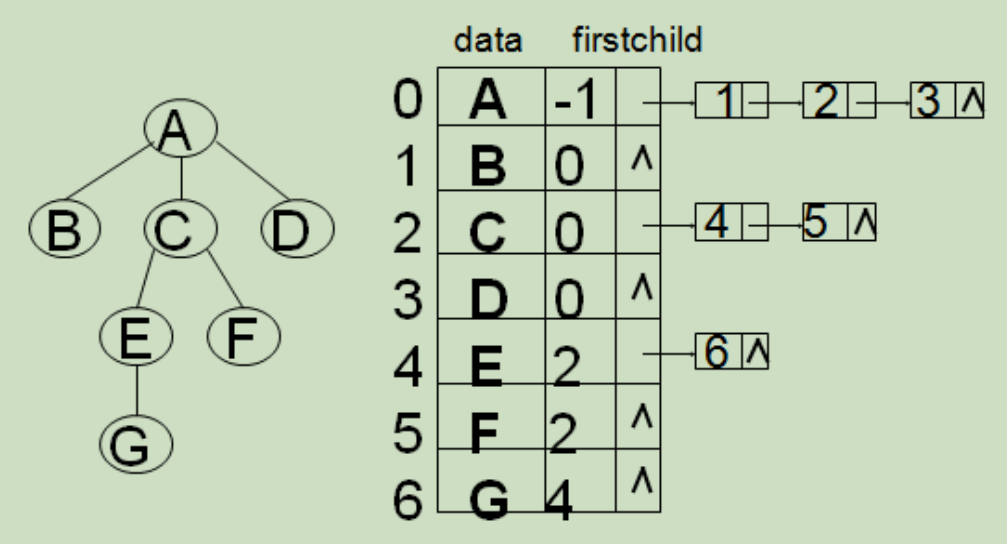
孩子表示法:
孩子结点结构:
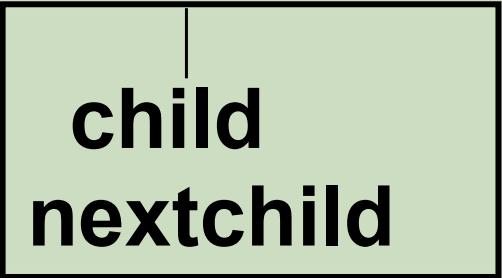
双亲结点结构:
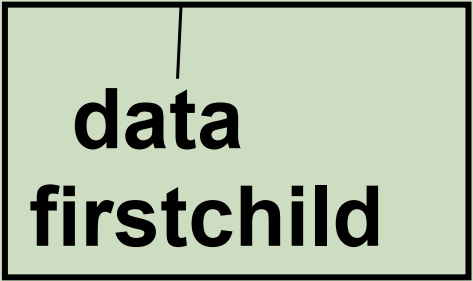
C 语言的类型描述:
typedef struct CTNode {
int child;
struct CTNode *nextchild;
} *ChildPtr;
typedef struct {
Elem data;
ChildPtr firstchild; // 孩子链的头指针
} CTBox;
typedef struct {
CTBox nodes[MAX_TREE_SIZE];
int n, r; // 结点数和根结点的位置
} CTree;3.树的二叉链表 (孩子-兄弟)存储表示法
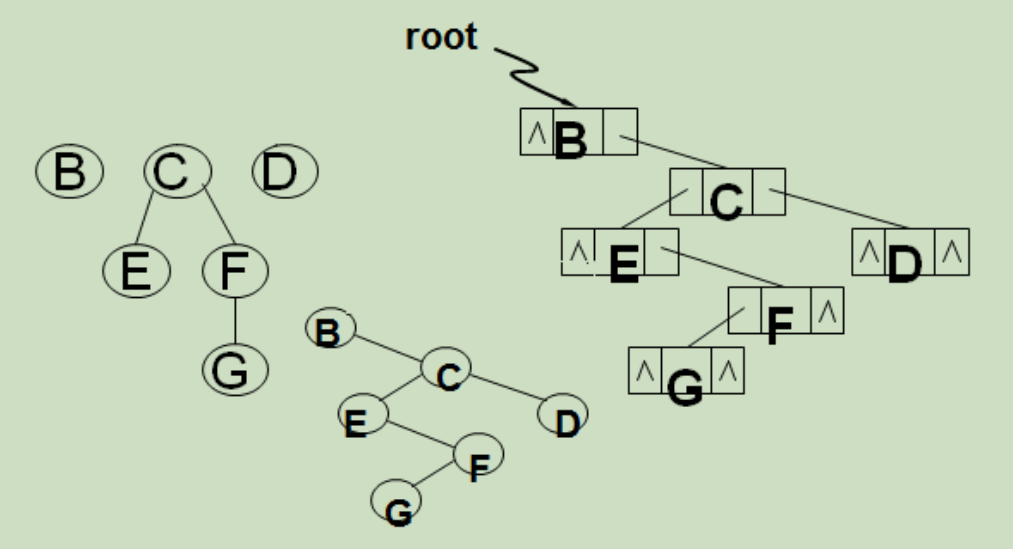
结点结构:

C 语言的类型描述:
typedef struct CSNode{
Elem data;
struct CSNode *firstchild, *nextsibling;
} CSNode, *CSTree;(二)森林和二叉树的转换
森林和二叉树的对应关系
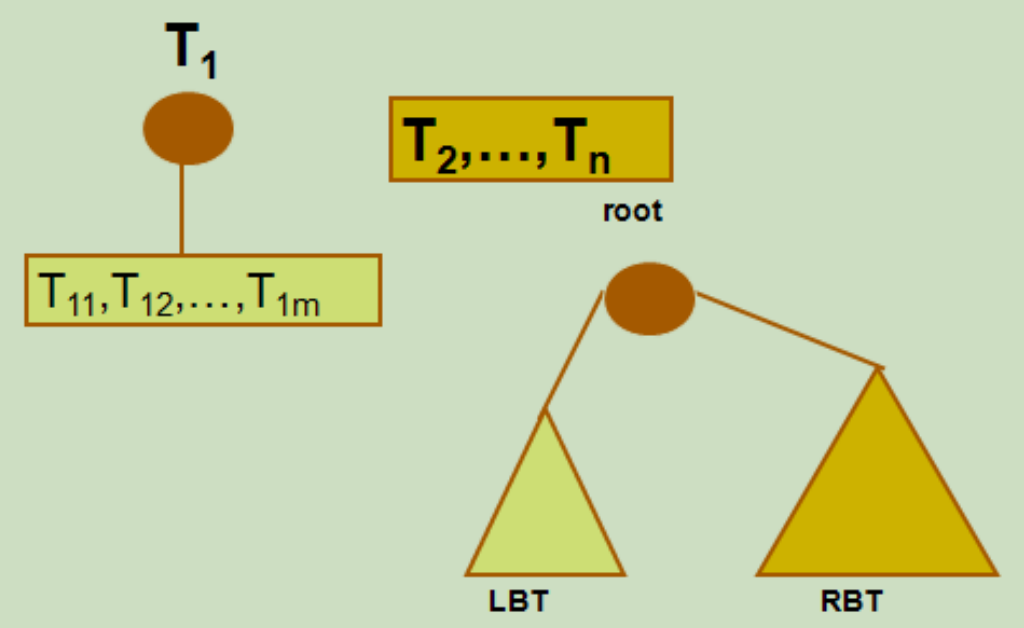
设森林 F = ( T1, T2, …, Tn );T1 = ( root,t11, t12, …, t1m );
二叉树 B =( LBT, Node(root), RBT );
由森林转换成二叉树的转换规则为:
若 F = Φ,则 B = Φ;否则,
由 ROOT( T1 ) 对应得到 Node(root);
由 (t11, t12, …, t1m ) 对应得到 LBT;
由 (T2, T3,…, Tn ) 对应得到 RBT。
由二叉树转换为森林的转换规则为:
若 B = Φ, 则 F = Φ;否则,
由 Node(root) 对应得到 ROOT( T1 );
由 LBT 对应得到 ( t11, t12, …,t1m);
由 RBT 对应得到 (T2, T3, …, Tn)。
由此,树和森林的各种操作均可与二叉树的各种操作相对应。
1. 树转换为二叉树
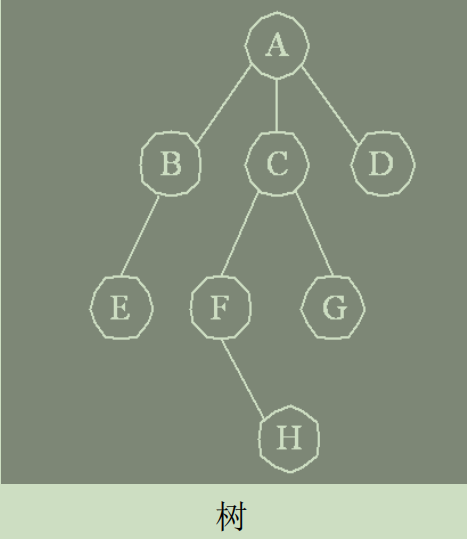
将一棵树转换为二叉树的思路, 主要根据树的孩子-兄弟存储方式而来的,方法是:
(1) 树中所有相邻兄弟之间加一条连线。
(2) 对树中的每个结点,只保留其与第一个孩子结点之间的连线, 删去其与其它孩子结点之间的连线。
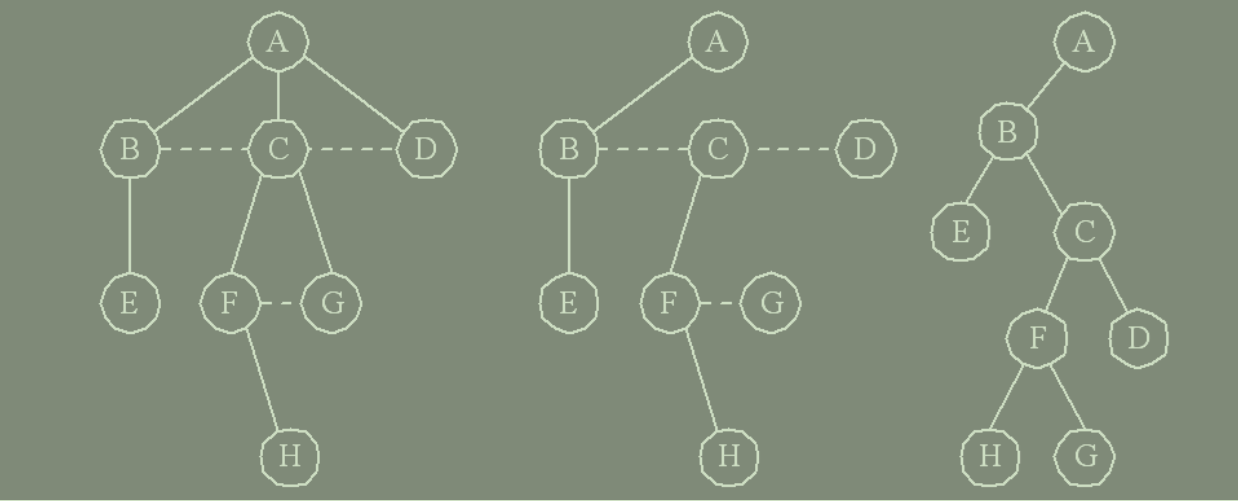
森林是若干棵树的集合。树可以转换为二叉树, 森林同样也可以转换为二叉树。
(1) 将森林中的每棵树转换成相应的二叉树。
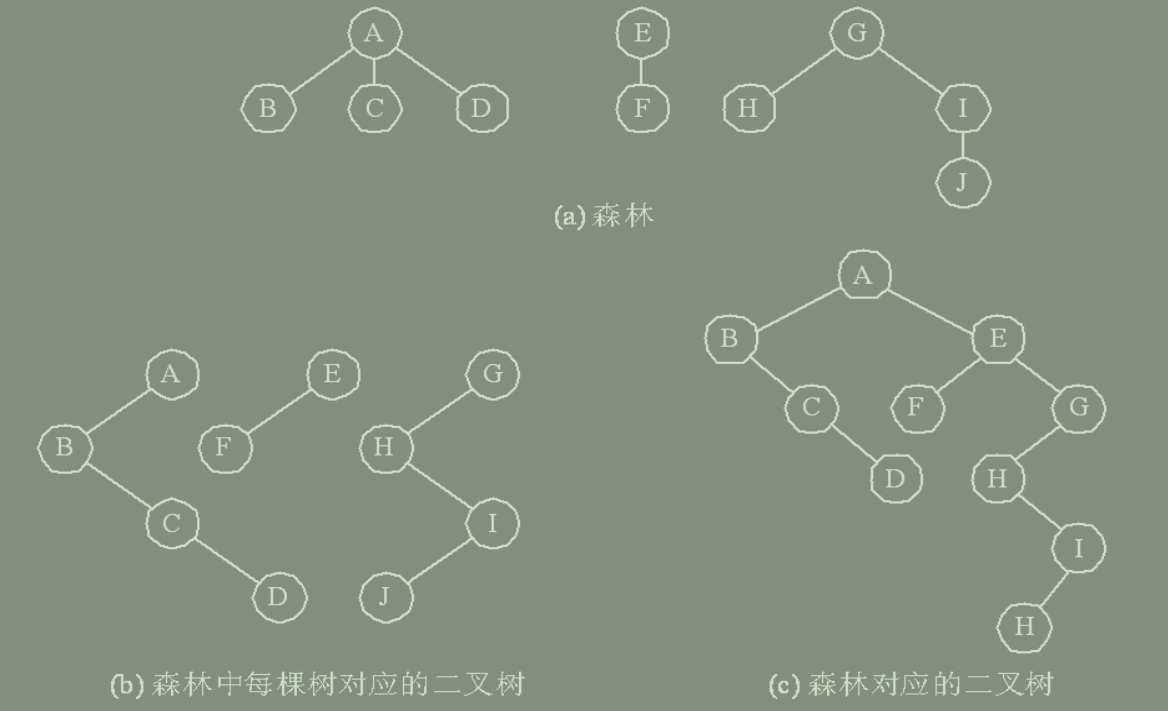
树和森林都可以转换为二叉树,二者的不同是: 树转换成的二叉树, 其根结点必然无右孩子,而森林转换后的二叉树,其根结点有右孩子。将一棵二叉树还原为树或森林,具体方法如下:
(1) 若某结点是其双亲的左孩子,则把该结点的右孩子、 右孩子的右孩子……都与该结点的双亲结点用线连起来。
(2) 删掉原二叉树中所有双亲结点与右孩子结点的连线。
(3) 整理由(1)、(2)两步所得到的树或森林, 使之结构层次分明。
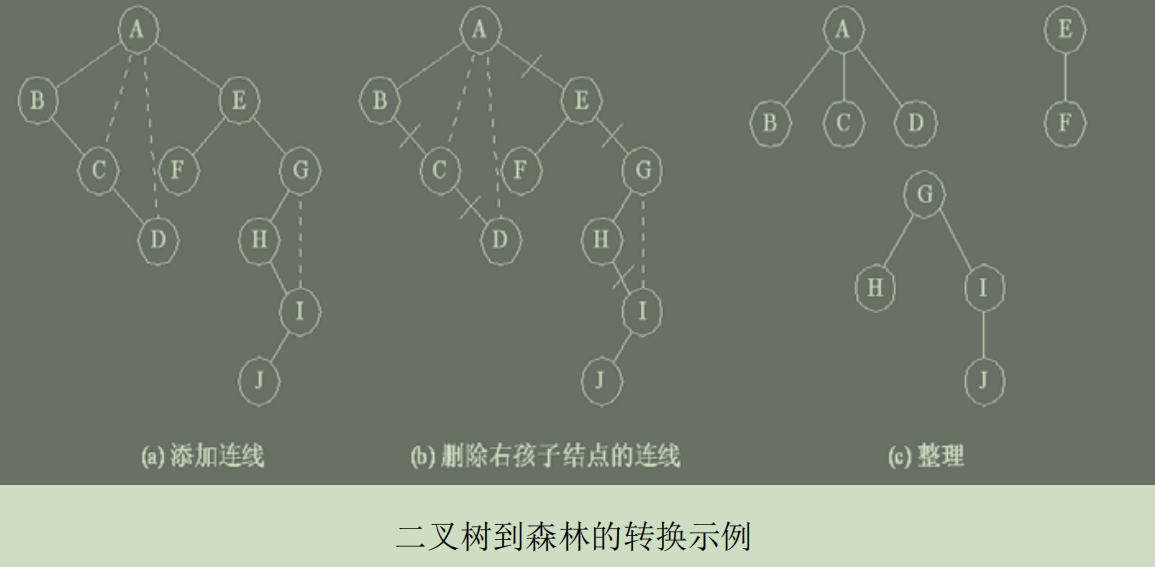
n 个结点的树有多少种形态?
树和森林的遍历
(一)树的遍历
1.先根(次序)遍历:若树不空,则先访问根结点,然后依次先根遍历各棵子树。
3.按层次遍历: 若树不空,则自上而下自左至右访问树中每个结点。
注:没有中序遍历
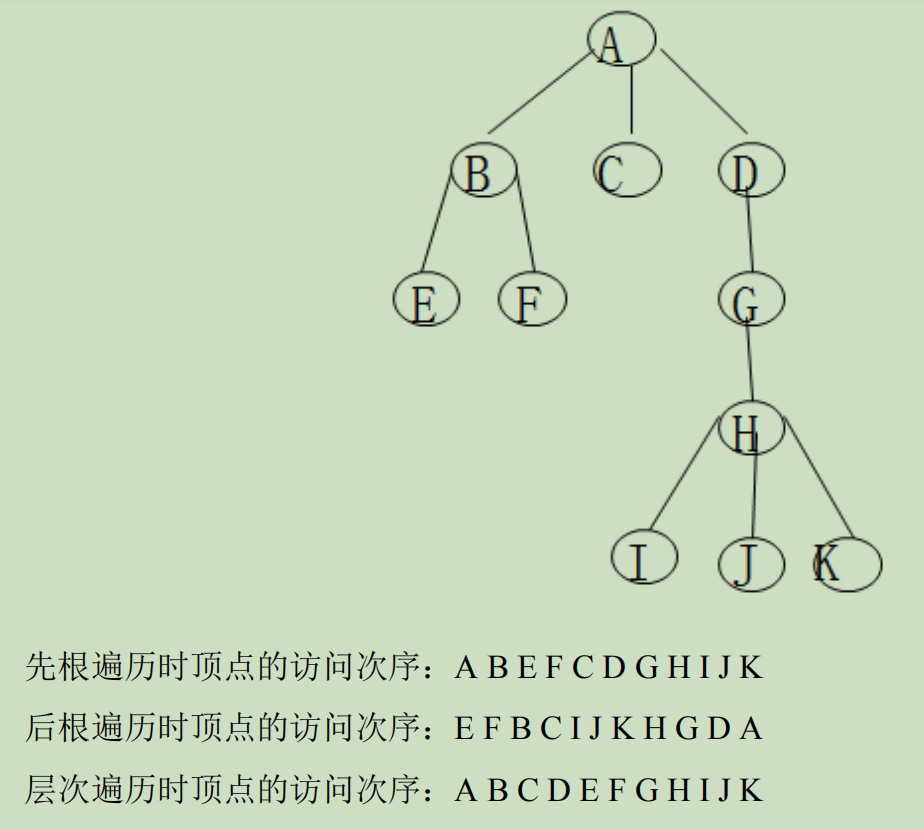
森林可以分解成三部分:
1)森林中第一棵树的根结点;
2)森林中第一棵树的子树森林;
3)森林中其它树构成的森林。
即:依次从左至右对森林中的每一棵树进行先根遍历。
2.后序遍历:若森林不空,则后序遍历森林中第一棵树的子树森林;访问森林中第一棵树的根结点;后序遍历森林中(除第一棵树之外)其余树构成的森林。
3.树的遍历和二叉树遍历的对应关系 ?
| 树 | 森林 | 二叉树 |
| 先根遍历 | 先序遍历 | 先序遍历 |
| 后根遍历 | 后序遍历 | 后序遍历 |
(三)树的遍历的应用
设树的存储结构为孩子兄弟链表
typedef struct CSNode{
ElemType data;
struct CSNode *firstchild, *nextsibling;
} CSNode, *CSTree;
int Depth(CSTree T){
if (T==NULL) return 0;
else{
d1 = Depth(T->firstchild);
d2 = Depth(T->nextsibling);
return Max{d1+1,d2}
}
}哈夫曼树与哈夫曼编码
(一)最优树的定义
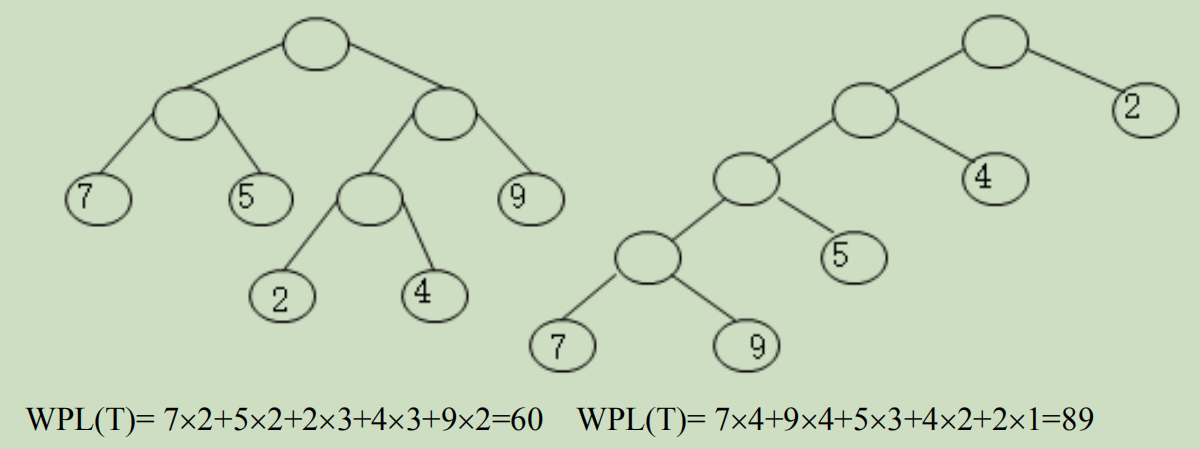
结点的路径长度定义为:从根结点到该结点的路径上分支的数目。
树的路径长度定义为:树中每个结点的路径长度之和。
在所有含 n 个叶子结点、并带相同权值的 m 叉树中,必存在一棵其带权路径长度取最小值的树,称为“最优树”。
(哈夫曼算法) 以二叉树为例:
2)在 F 中选取其根结点的权值为最小的两棵二叉树,分别作为左、右子树构造一棵新的二叉树,并置这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和;
4)重复 (2) 和 (3) 两步,直至 F 中只含一棵树为止。
(三)哈夫曼编码
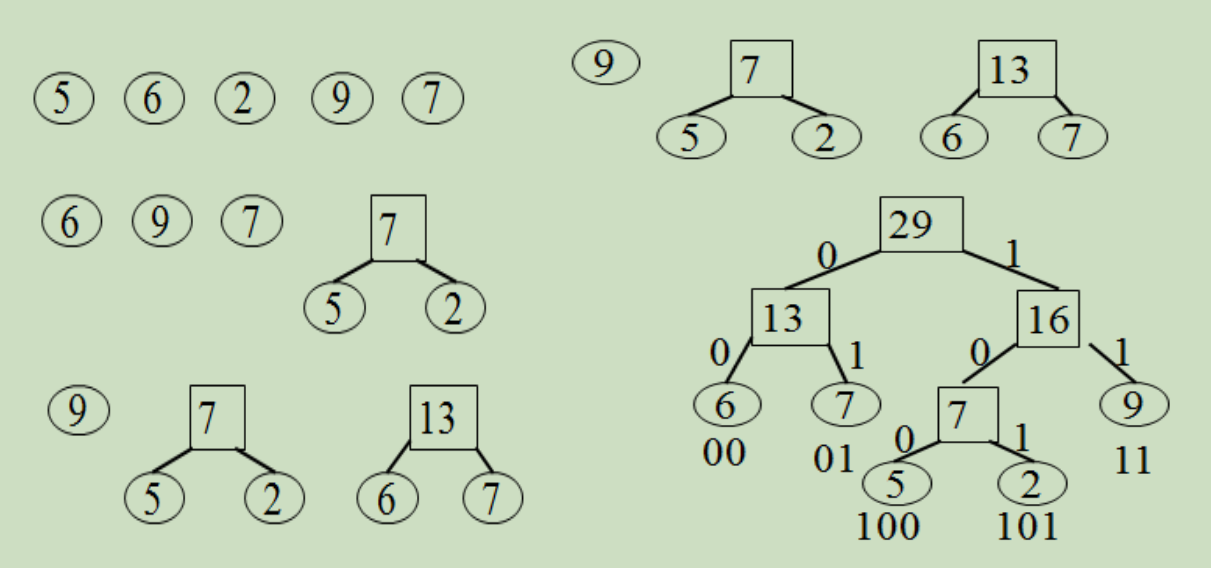
例如: 已知权值 W={ 5, 6, 2, 9, 7 }
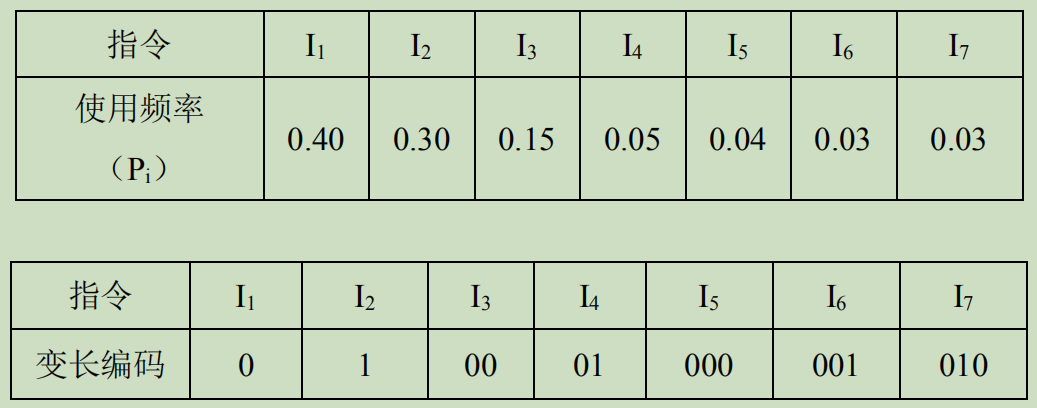
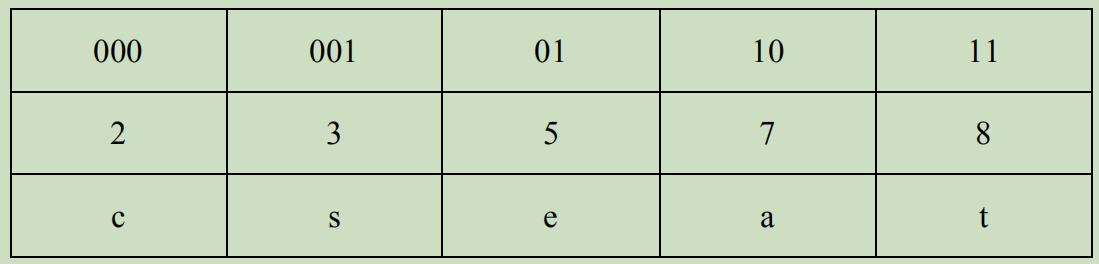
若要设计长短不等的编码,则必须是任一个字符的编码都不是另外一个字符编码的前缀,这种编码称做前缀编码。
首先规定二叉树的构造为左走 0,右走 1。

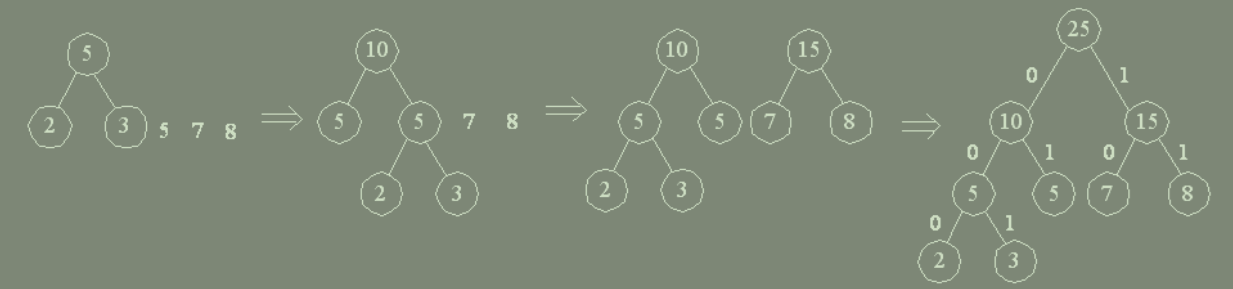
按规定:左 0 右 1,则有
前述构造满足赫夫曼编码的最短最优性质:
② 将所有字符变成二进制的赫夫曼编码,使带权路径长度最短。
1.构造哈夫曼树的常见错误:在合并中不是选取根结点权值最小的两棵二叉树(包括已合并的和未合并的),而是选取未合并的根结点权值最小的一棵二叉树与已经合并的二叉树合并。
2.对哈夫曼树的总结:
(2)哈夫曼树中没有度为 1 的结点,因为非叶子结点都是通过两个结点合并而来。但是,没有度为 1 的二叉树并不一定是哈夫曼树。
(3)用 n 个权值(对应 n 个叶子结点)构造的哈夫曼树,形态并不是唯一的。
(1)哈夫曼编码是能使电文代码总长最短的编码方式。此结论由哈夫曼树是带权路径长度最小的树的特征可得。
(2)哈夫曼编码是一种前缀编码,保证其在译码时不会产生歧义。因为,在哈夫曼编码中,每个字符都是叶子结点,而叶子结点不可能从根结点到其他叶子结点的路径上,所以一个字符的哈夫曼编码不可能是另一个字符的哈夫曼编码的前缀。
本章学习重点
1. 熟练掌握二叉树的结构特性,了解相应的证明方法。
3. 遍历二叉树是二叉树各种操作的基础。实现二叉树遍历的具体算法与所采用的存储结构有关。掌握各种遍历策略的递归算法,灵活运用遍历算法实现二叉树的其它操作。层次遍历是按另一种搜索策略进行的遍历。
5. 熟悉树的各种存储结构及其特点,掌握树和森林与二叉树的转换方法。
亲爱的读者:有时间可以点赞评论一下
作者其它文章
- 数字图像处理
- 剑指offer2
- 工作学习
- 这些算法有自己的方法
- 插件
- 软件使用
- 数学
- mybatis
- 计算机网络
- 正则表达式专栏
- 问题记录
- Thymeleaf
- zuul
- hystrix
- 正则表达式
- feign
- 编程相关技术
- ribbon
- 微服务
- eureka
- 分布式
- 模板
- angularjs
- javascript
- html
- c++ grammar
- c grammar
- python grammar
- java grammar
- 软件工程
- 数据库系统概论
- 转载
- 小知识
- 考研
- webservice
- 网络
- struts2
- springmvc
- springboot
- redis
- mongodb
- hibernate
- 计算机组成原理
- 当代世界经济与政治
- leetcode
- 思想道德修养与法律基础
- 毛泽东思想和中国特色社会主义理论体系概论
- 作乐
- 生活点滴
- 娱乐
- 中国近现代史纲要
- 操作系统
- sunny day, singing day
- 设计模式与算法
- 框架
- 概率论与数理统计
- 线性代数
- JAVA
- 前端
- 数据库
- 马克思主义基本原理概论
- 软考
- 生活,生,活
- 晴雨
- CSS
- LINUX
- java web整合开发王者归来
- 英语
- 高等数学
- 数据结构


















全部评论