作者：whisper

链接：http://proprogrammar.com:443/article/105

声明：请尊重原作者的劳动，如需转载请注明出处

    说明：本章是概率论的基础内容，概念比较多，特别要注意对概念的准确理解，仔细辨析概念间的差别，本章的重点是事件的关系，独立性的概念，条件概率的定义与计算，特别要重视全概率公式，贝叶斯公式的思想。

    随机试验

    样本空间

    样本点

    随机事件

    文氏图

    事件的关系及运算

    关系

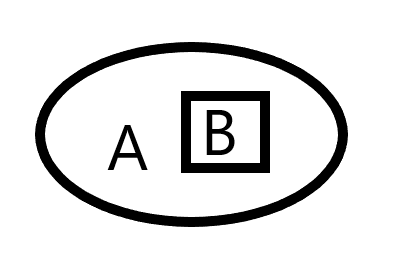
    包含（子事件）：B ⊂ A或者A ⊃ B

    概率意义：A发生必导致B发生

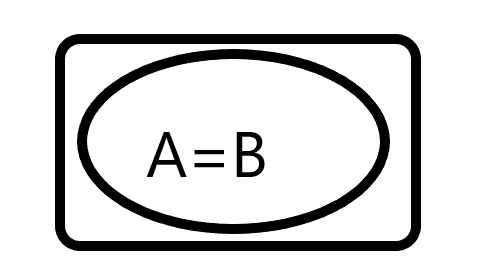
    相等：A=B

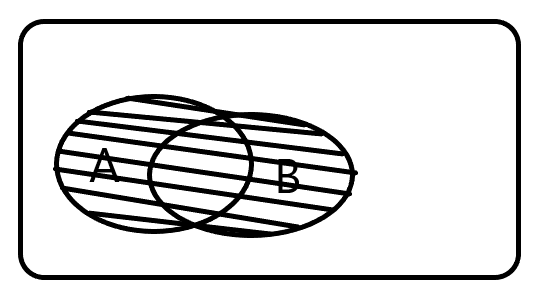
    并（和）事件：记A ∪ B或A+B

    概率意义：A发生或者B发生<=>A，B中至少有1个发生

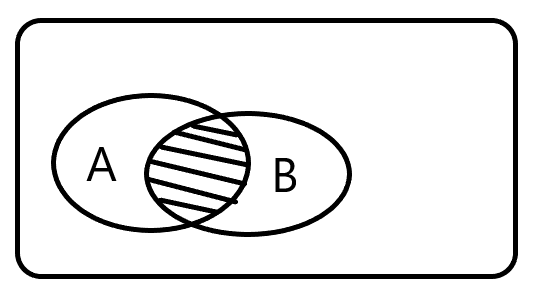
    交（积）事件，记A ∩ B或AB

    概率意义：A发生且B发生；A，B同时发生

    差事件，记A-B = A┐B=A - AB

    概率意义：A发生且B不发生

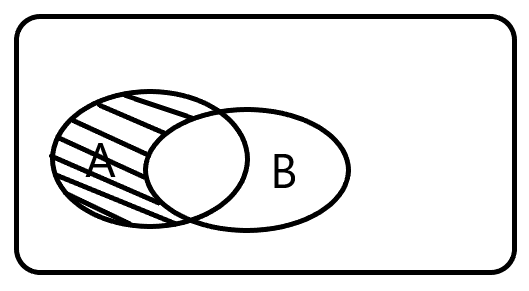
    A与B互不相容（互斥）：AB = Φ

    概率意义：A，B不能同时发生

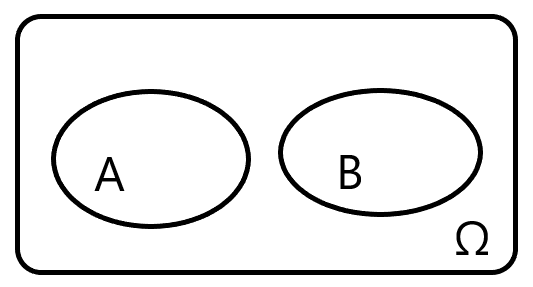
    A与B对立：AB = Φ且A ∪ B = Ω

    概率意义：A，B不能同时发生但必有一个发生

    注：对立一定互斥，互斥不一定对立

    摩根律

    ┐(A∪B) = ┐A ∩ ┐B           ┐(A∩B) = ┐A ∪ ┐B 

    频率与概率

    概率统计意义

    概率公理化定义

    概率的基本性质与公式

    性质i：对于不可能事件Φ，则P(Φ) = 0

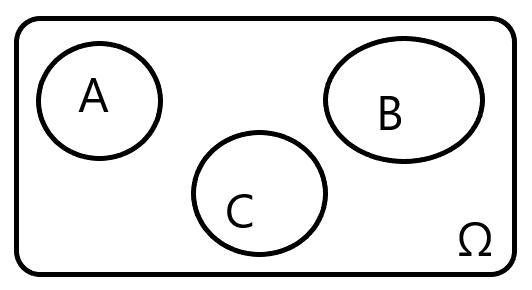
    性质ii：有限可加性

                A₁，A₂，A₃两两互不相容，则P(A₁∪A₂∪A₃) = P(A₁) + P(A₂) + P(A₃)

    性质iii：单调性

                设A⊂B，则有P(B-A) = P(B) - P(A) ≥ 0 => P(B) ≥ P(A)

    性质iv： ∀A，有0≤P(A)≤1

    性质v：对立求逆

                P(┐A) = 1 - P(A)    思想：正难则反

    性质vi：加法公式

    P(A∪B) = P(A) + P(B) - P(AB)，特别的，当AB=Φ，P(A∪B) = P(A) + P(B)

    三事件加法公式

    P(A∪B∪C) = P(A) + P(B) + P(C) - P(AB) - P(AC) - P(BC) + P(ABC)

    补充性质vii：减法公式

    P(B-A) = P(B) - P(AB) = P(B┐A)，特别的，若A⊂B，则P(B-A) = P(B) - P(A)

    等可能概型

    概率的古典定义（古典概型）

    随机试验E具有以下两个特征，称E为古典型试验

    （1）所涉及的随机事件只有有限个样本点（有限性），譬如n个

    （2）每个基本事件出现的可能性是相等的（等可能性），若有n个，则每个发生概率为1/n

    若事件A含有k个样本点，则事件A的概率为

                     P(A) = 事件A所含样本点的个数/Ω中所有样本点的个数 = k/n

    排列数 A(n, m)

    组合数 C(n, m) = A(n, m)/m! = n!/[m!*(n-m)!]

    补充：几何概型

    （1）样本点无限个

    （2）样本点等可能性

    对应于长度或面积

    P(A) = A的长度或面积/Ω的长度或面积

    条件概率

    对于任意两个事件A，B，其中P(A)>0，“事件A发生的条件下B发生的概率”，简称为“事件B关于A的条件概率”，定义为

                                                     P(B|A) = P(AB)/P(A)

    对于固定的事件A，条件概率P(B|A)具有概率的一切性质，即

    （1）（非负性）0 ≤ P(B|A) ≤ 1

    （2）（规范性）P(Ω|A) = 1

    （3）（可列可加性）如果事件B₁，B₂，... 互不相容，那么P((B₁∪B₂∪...)|A) = ∑(i=1，n）P(Bᵢ|A)

    计算条件概率方法

    方法1 用定义 P(B|A) = P(AB) / P(A)

    方法2 用缩小样本空间    Ω->A

    注：P(B|A) 与 P(B) 的大小关系不确定

    乘法公式

    设A、B为两个事件，若P(A)>0，则有

                                     P(AB) = P(A)P(B|A)

    若P(B)>0，则有

                                    P(AB) = P(B)P(A|B)

    一般地，若P(A₁A₂...Aₙ₋₁)>0，则有

                                    P(A₁A₂...Aₙ₋₁Aₙ) = P(A₁)P(A₂|A₁)P(A₃|A₁A₂)...P(Aₙ|A₁A₂...Aₙ₋₁)

    注：P(B|A) = 1 - P(┐B|A)

    定义（划分、完备事件组）若事件组B₁,B₂,...Bₙ满足下列条件：

    （1）BᵢBⱼ = Φ，i ≠ j；i, j = 1, 2... n；

    （2）B₁∪B₂...∪Bₙ = Ω

    则称B₁，B₂...Bₙ是一个完备事件组或称为事件组B₁，B₂...Bₙ为Ω的一个分割（也称为划分，部分）

    全概率公式

    设B₁，B₂...Bₙ是一个完备事件组，P(Bᵢ)>0，i = 1, 2...n，则对任意的事件A有：

                                  P(A) = ∑(i=1, n)P(Bᵢ)P(A|Bᵢ)

    证明:

    P(A) = P(AB₁∪AB₂...∪ABₙ) = P(AB₁) + P(AB₂) + ... + P(ABₙ) = P(B₁)P(A|B₁) + P(B₂)P(A|B₂) + ... + P(Bₙ)P(A|Bₙ)

    贝叶斯公式

    设B₁,B₂....Bₙ是一个完备事件组，P(Bᵢ)>0，j = 1, 2, ... ,n，对任意的事件A，P(A)>0，则

                     P(Bᵢ|A) = [P(Bᵢ)P(A|Bᵢ)] / [∑(i=1, n)P(Bᵢ)P(A|Bᵢ)]

    说明：即P(Bᵢ|A) = P(ABᵢ)/P(A)，上面是乘法公式的变形，下面是全概率公式，贝叶斯公式也称逆概公式

    独立性

    定义（两事件）若A，B的概率满足P(AB) = P(A)P(B)，称A与B独立

    注：独立是一个概率关系

    定理一

    设A、B是两事件，且P(A) > 0，若A、B相互独立，P(B|A) = P(B)，反之亦然

    定理二

    若事件A与B相互独立，则下列各对事件也相互独立

                         ┐A与B、A与┐B，┐A与┐B

    三事件独立性

    如果事件A、B、C满足

                        P(AB) = P(A)P(B)

                        P(BC) = P(B)P(C)

                        P(AC) = P(A)P(C)

                        P(ABC) = P(A)P(B)P(C)

    同时成立，则称三事件A，B，C相互独立，若A，B，C仅满足前三个等式，则称A，B，C两两独立。注意：“n个事件相互独立”与“n个事件两两独立”并非一回事。

    小技巧：对于既出现原概率又也现逆概率的情况，要想到使用减法公式，如

                     P(A┐B) = P(A) - P(AB)

    典型问题：抽奖问题，中奖的概率与抽奖的次序无关，每个人中奖的概率都是相同的

亲爱的读者：有时间可以点赞评论一下