作者：whisper

链接：http://proprogrammar.com:443/article/143

声明：请尊重原作者的劳动，如需转载请注明出处

    平面图形的面积

    1、直角坐标情形

    （1）由曲线y = f(x) (f(x) >=0)及直线x = a, x = b (a < b)与x轴所围成的平面图形的面积A是定积分

                                          A = ∫[a, b]f(x)dx

    其中被积表达式f(x)dx就是直角坐标下的面积元素，它表示高为f(x)，宽为dx的矩形的面积

    （2）由曲线x = f(y) (f(y) >= 0)及直线y = a, y = b(a < b)与y轴所围成的曲边梯形的面积A是定积分

                                         A = ∫[a, b]f(y)dy

    其中被积表达式f(y)dy就是直角坐标下的面积元素，它表示高为f(y)，宽为dy的矩形的面积

    直角坐标情形推广

    （1）由曲线y = f(x)，y = g(x)及直线x = a与x = b(a < b)所围成图形的面积

                                      S = ∫[a, b]|f(x) - g(x)|dx

    （2）由曲线x = f(y)，x = g(y)及直线y = a与y = b(a < b)所围成图形的面积

                                      S = ∫[a, b]|f(y) - g(y)|dy

    总结：找准区域，进行积分

    2、极坐标情形

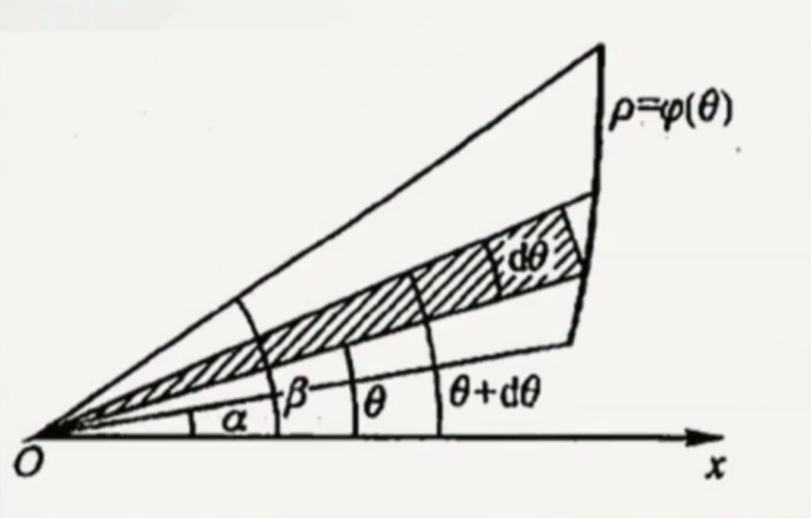
    设由曲线ρ = φ(θ)，及射线 θ = α， θ = β围成一图形（简称为曲边扇形）

    取极角θ为积分变量，它的变化区间为[α, β]

    相应于任一小区间[θ, θ + dθ]的窄曲边扇形的面积可以用

    半径为 ρ = φ(θ) ，中心角为 ρ = φ(θ) 的扇形的面积来近似代替，

    从而得到这窄曲边扇形面积的近似值，即曲边扇形的面积元素

                                                      dA = (1/2)[φ(θ)]²dθ

    体积

    1、旋转体的体积

    （1）由连续曲线y = f(x)，直线x = a, x = b及x轴所围成的曲边梯形绕x轴旋转一周成的立体

    取横坐标x为积分变量，这的变化区间为[a, b]

    相应于[a, b]上的任一小区间[x, x + dx]的窄曲边梯形绕x轴旋转而成的薄片的体积，近似于以f(x)为底半径，dx为高的扁圆柱体的体积

    即体积元素

                                                    dV = π[f(x)]²dx

    以π[f(x)]²dx为被积表达式，在闭区间[a, b]上作定积分，便得所求旋转体的体积为

                                                   V = ∫[a, b]π[f(x)]²dx

    （2）由连续曲线x = f(y)，直线y = a, y = b (a < b)与y轴所围成的曲边梯形绕y轴旋转一周而成的立体

                                                   V = ∫[a, b]π[f(y)]²dy

    （3）由平面图形0 <= a <= x <= b， 0 <= y <= f(x)绕y轴旋转所成的旋转体的体积为

                                                    V = ∫[a, b]2πxf(x)dx

亲爱的读者：有时间可以点赞评论一下